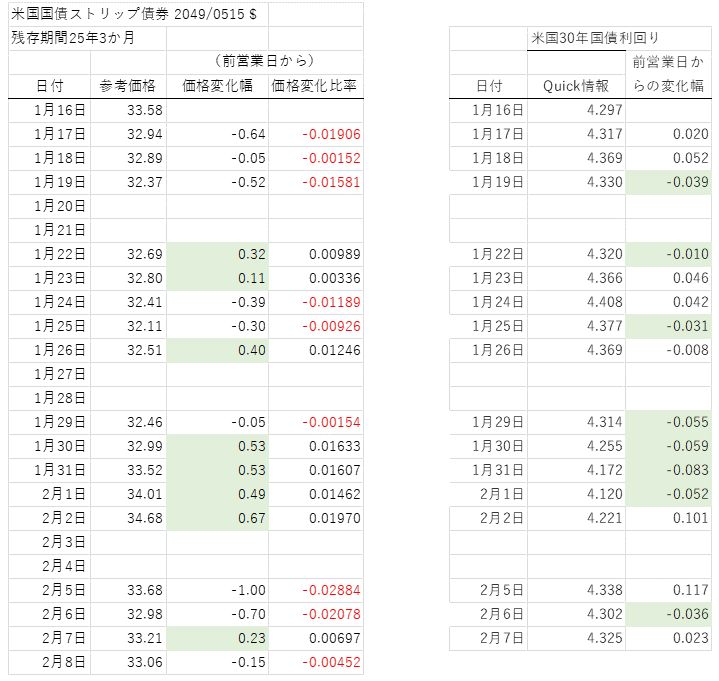
前回(株式投資の考え方:2024年8月の株価暴落から学べること)は、日経平均の変化を、夜間の変化と日中の変化に分解してみました。
その結果、通常時は夜間の変化と日中の変化の関連性(相関)は小さい。しかし、8月2日と8月5日は、夜間に大きく下落し、日中にさらにその下落幅が大幅に拡大した結果暴落となったことが分かりました。
夜間取引は日経平均先物取引(シカゴ市場や大阪市場)になります。この夜間取引には米国市場の取引が影響を与えているかもしれません。そこで、視野を少し広げて、ダウ平均、S&P500、NASDAQという米国市場を代表する3つのインデックスと日経平均の動きがどのように関係しているかを調べてみます。
最初に、日経平均と米国の3つのインデックスについて、6月6日から8月16日までの50営業日の基本統計量を確認すると、次のようになります。
範囲/平均値27.8%6.6%8.8%13.9%
|
日経平均 |
ダウ平均 |
S&P 500 |
NASDAQ |
| 平均値 |
38,715.42 |
39,616.43 |
5,464.18 |
17,585.50 |
| 標準偏差 |
2,090.39 |
724.93 |
106.555 |
593.72 |
| 最小 |
31,458.42 |
38,589.16 |
5,186.33 |
16,195.806 |
| 最大 |
42,224.02 |
41,198.08 |
5,667.2 |
18,647.448 |
| 範囲 |
10,765.6 |
2,608.92 |
480.87 |
2451.642 |
※数値絶対値の単位:日経平均は円、米国インデックスはドル。以下、同様です。
ざっと見ると日経平均は他のインデックスと比べてかなり変動幅が大きくなっています。これは範囲(最高値と最安値の幅)を平均株価で割ってみると分かります。
この50営業日の間で、日経平均は平均値の上下に27.8%も変動しています。それに対してダウ平均が6.6%、S&P500が8.8%と小さく、NASDAQでも13.9%で変動幅は日経平均の半分でした。
次にこの4つのインデックスの動きを比較してみます。それぞれの変動範囲が異なるので、各インデックスの毎日の株価を偏差値に換算してからチャートに表してみます。(このチャートは各株価インデックスを平均からの偏差値に換算したものなので、変動の大きさの絶対値を表していません。ご注意ください。)
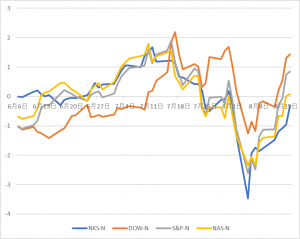
この図をみると、ダウ平均は、他のインデックスとはかなり異なる動きをしています。それに対して、他の3種のインデックスは比較的似た動きをしています。
そこでこの4つのインデックスの相関係数を求めてみると次の表のとおりです。
|
日経平均 |
ダウ平均 |
S&P 500 |
NASDAQ |
| 日経平均 |
1 |
|
|
|
|
| ダウ平均 |
0.22 |
1 |
|
|
| S&P 500 |
0.84 |
0.51 |
1 |
|
| NASDAQ |
0.91 |
0.22 |
0.94 |
1 |
日経平均とNASDAQの動きがかなり似ています。米国株同士ではS&P500とNASDAQの動きが似ていますが、これはS&P500の中にNASDAQの有力銘柄が含まれているので自然です。
一方、日経平均とダウ平均は、この期間で見る限り、あまり連動していません。
上の表は日経平均と同じ日付の米国インッデクスとの相関を調べたものです。時差を加味すると日経平均の動きが米国株に影響を与えているかという観点で見ていることになります。そこで、米国株の動きが日経平均に影響を与えているかという観点で見るため、1日前、2日前の米国株インデックスと日経平均の相関も調べてみました。
|
ダウ平均 |
S&P 500 |
NASDAQ |
| 同日 |
0.22 |
0.84 |
0.91 |
| 1日前 |
0.14 |
0.81 |
0.89 |
| 2日前 |
0.01 |
0.70 |
0.82 |
この表からは、日経平均と同日の米国株インデックスの相関が最大で、日経平均と前日の米国株インデックスの相関は少し小さく、日経平均と前々日の米国株インデックスの相関はさらに小さくなっています。このことから、この分析期間中は米国株インデックスが日経平均の下落の影響受けて下落した傾向もあると言えるでしょう。
株価の動きのまとめ
さて、この50営業日の株価の動きと上で調べた結果から考えられることをまとめてみます。
1.8月16日までの50営業日では、日経平均とNASDAQの変動は似通った動きをした。
2.変動の幅ではNASDAQより日経平均が2倍程度大きかった。
3.NASDAQは7月10日に最高値を付けてその後下落を始めた。一方、日経平均は7月11日に最高値を付けて下落を始めた。日経平均の動きがNASDAQに1日遅れていることから、この時点では日経平均はNASDAQの下げを追随しているようです。
4.両者は7月最終週まで下落傾向にあったが、7月31日に日銀が利上げを発表した時点では一旦少し上がった。
5.翌8月1日から日経平均は3日連続で合計7,643.40円下げ(7月31日終値の約20%の下げにあたる)。この間NASDAQも3日連続で合計1,399.32円の下げとなった。これは7月31日終値の約8%の下げにあたるのでNASDAQの動きは日経平均に同調したが変動幅ははるかに小さかった。
6.日経平均は8月5日に31,458.42円で底となり、その後、8月16日までで5,255.16円上げた。NASDAQは8月7日の16,195.806ドルが底となり、その後、8月16日までで1,435.914ドル上げて、既に7月31日の株価を上回った。
ダウ平均はNASDAQとは異なる動きをしています。恐らく、投資資金の一部がNASDAQ銘柄からダウ銘柄に移動しているのでしょう。
なお、いうまでもないことですが、日米株価の相関が高いことは因果関係があることを示しているわけではありません。日米両方の市場で投資活動を行っているグローバル投資家が日米両方の市場で同じような売り買いをしているためでしょう。
こうしてみると、8月1日からの株価の下げは株価だけをみるだけでは原因が分かりません。恐らく、7月11日のNASDAQ急落以降の下げのダメージに加えて、日銀利上げによる円高ショックが8月5日の暴落の原因なのでしょう。特に日本株については、為替レートの変動が大きい影響を与えているようです。
連載
初回:株式投資の考え方:株価の暴落にどう対処するか
2回目:株式投資の考え方:2024年8月の株価暴落から学べること
3回目:株式投資の考え方:2024年8月の株価暴落はどのように起きたのか?(本記事)
4回目:株式投資の考え方:良い会社とはどのような会社か、投資先候補銘柄の選定法
5回目:株式投資の考え方:いつ買い・いつ売るか
6回目:株式投資の考え方:投資成績の評価方法
7回目:株式投資の考え方:投資成績の評価方法ー実例